Theoretical modelling for kesterite photovoltaics
Adam J. Jackson, Aron Walsh
a.j.jackson@bath.ac.uk
Wednesday 18 Nov 2015
1 Introduction
(This presentation is online at https://wmd-bath.github.io/theory4kest)
1.1 About me
- Adam J. Jackson
- Undergraduate MEng Chemical Engineering (Bath, UK)
- Doctoral Training Centre in Sustainable Chemical Technologies (Bath, UK)
- Currently writing up a PhD thesis
- "Ab initio thermodynamics for practical kesterite photovoltaics"
- Based at University of Bath
- Near Bristol, < 2 hours from London
1.2 University of Bath

1.3 Kesterites at Bath
- Early experimental work
- Laurie Peter (my co-supervisor)
- Jonathan Scragg, Phillip Dale, Diego Columbara
- Laurie Peter (my co-supervisor)
- Current/recent
- Aron Walsh [computational]
- Adam Jackson, Jarvist Frost, Suzy Wallace
- Mark Weller [crystallography, solid-state synthesis]
- Mako Ng
- Laurie Peter, Kieran Molloy [solution processing]
- Anna Sudlow, Gabriela Kissling
- Aron Walsh [computational]
- PVTEAM partners
- SPECIFIC, Bristol, Loughborough, Northumbria
1.4 Aims of this talk
- Introduce the main theoretical methods that are relevant to kesterites research
- Highlight key existing theoretical work
- Identify problematic areas and opportunities for collaboration
- Help with terminology and critical reading of literature
1.5 Not in this talk
- Nuts and bolts of running calculations
- Device modelling
2 The "cheat sheet"
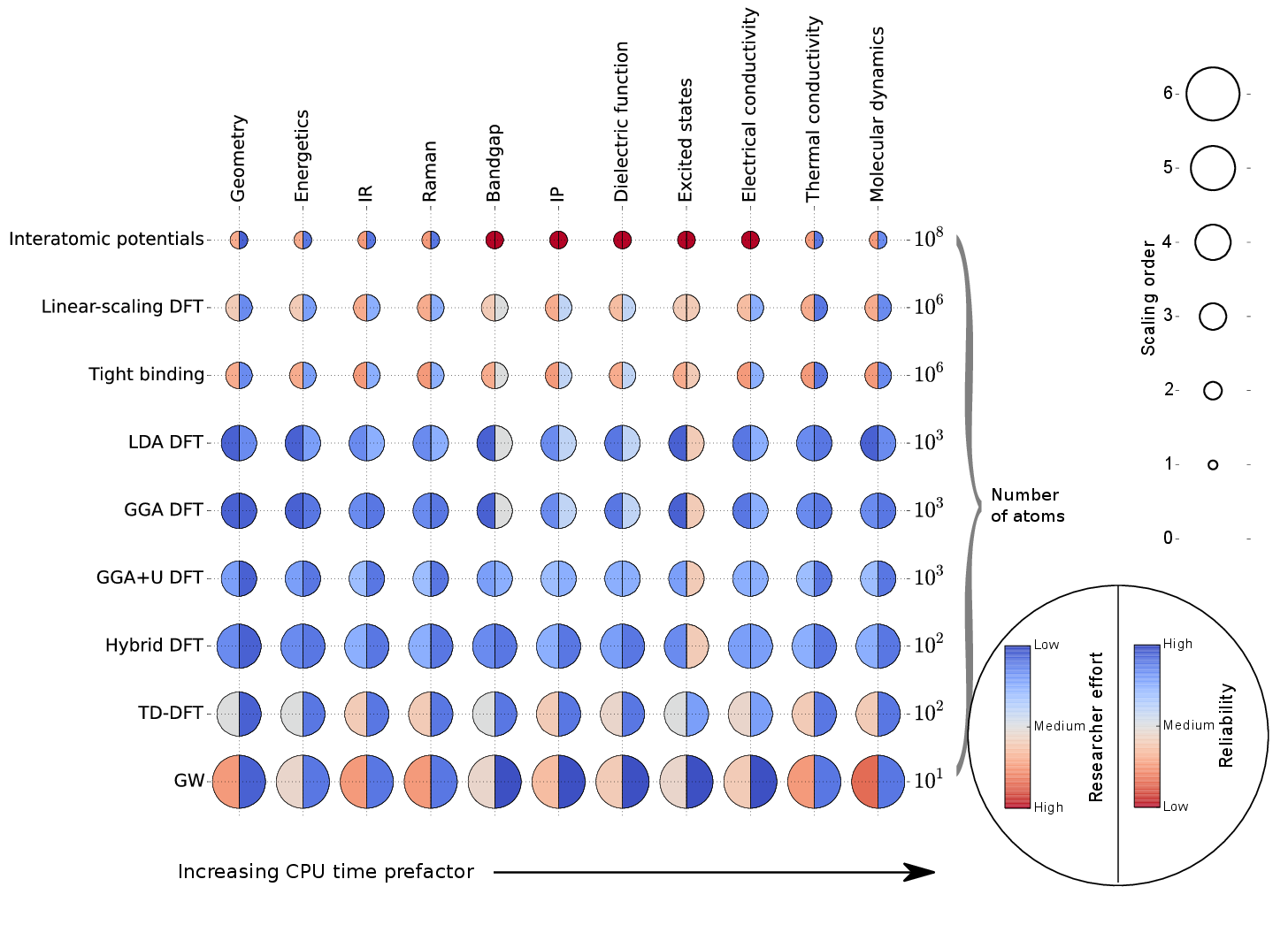
3 Atomistic methods
3.1 Interatomic potentials
- Simple interaction functions such as Buckingham potentials \((V = Ae^{-Br} - \frac{C}{r^6})\)
- Polarisation can be included approximately through shell models
- Simple to implement, inexpensive calculations
- Main challenge is in fitting the potentials
- No information about electronic structure
- We have access to a parameterisation for CZTS (Chris Eames, University of Bath)
3.2 Ab initio methods
- Focus on time-independent Schrödinger equation \(H\Psi = E\Psi\)
- (Time-dependent methods exist, are more complicated…)
- Solution for a system locates the ground state configuration and energy
- Ground state energy \(E \approx U(T=0)\)
- \(H\) is an operator, must be defined for a particular basis
- Bloch's theorem:
- The single-electron eigenvectors in a periodic system are the products of a single function with the periodicity of the lattice and all the points of the reciprocal lattice
- Crystalline systems can be modelled with a periodic boundary condition
- but the sum over the reciprocal lattice must be converged
- (integration over the Brillouin zone)
- but the sum over the reciprocal lattice must be converged
3.3 Ab initio codes
- A wide range of packages are available
- Wikipedia maintains a handy table
- Most popular codes include
- VASP (very efficient, if archaic, code for periodic systems)
- Gaussian (fast and quite user-friendly, non-periodic)
3.4 Density Functional Theory
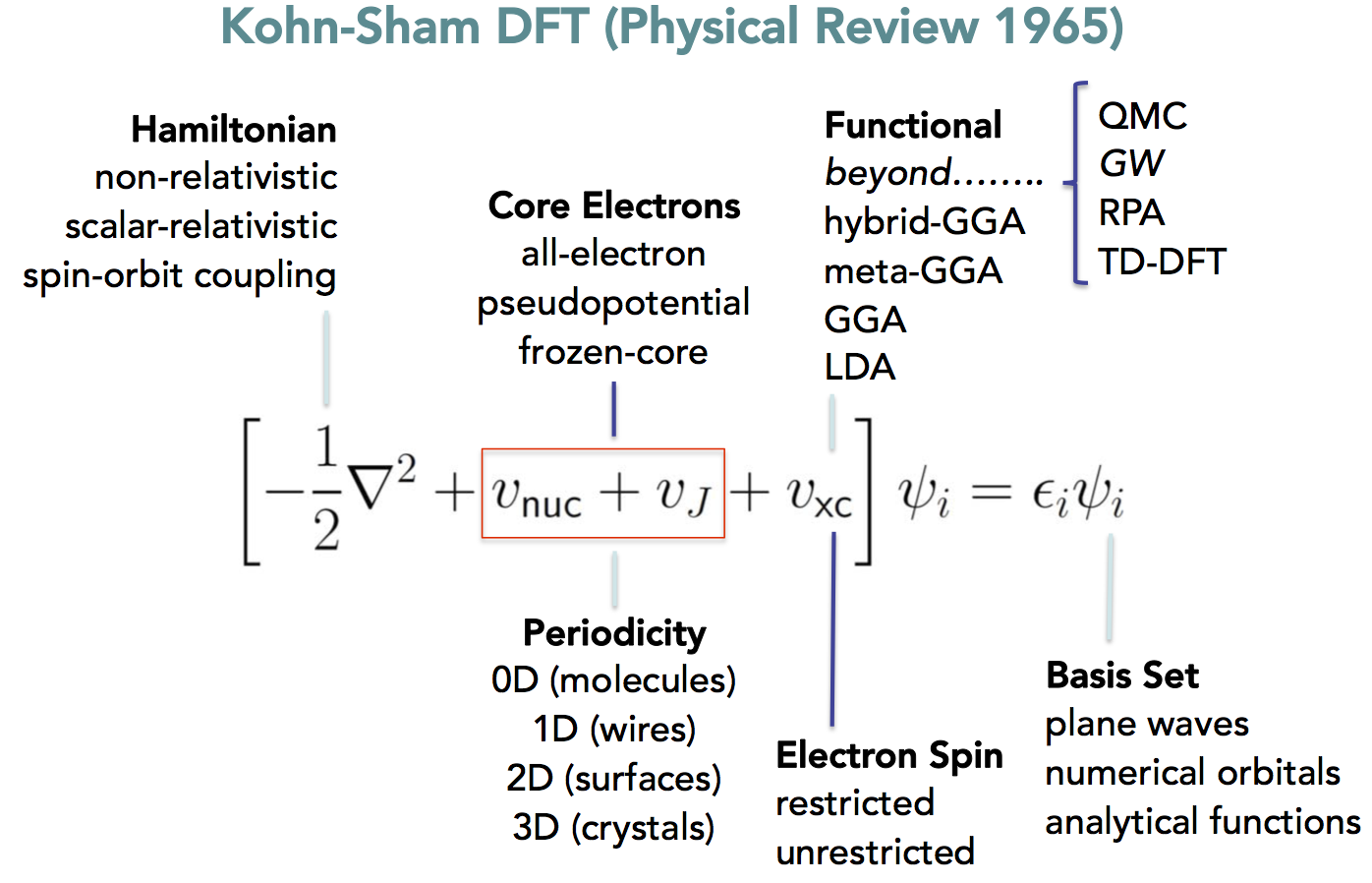
- Kohn-Sham DFT replaces \(E_{XC}(\Psi)\) with \(E_{XC}(\mathbf{\rho})\)
- Accuracy of DFT calculation depends on
- Numerical convergence of iterations
- Convergence of basis set, k-points
- Quality of XC-functional
- Does not "converge" systematically
- "Jacob's ladder" of methods 10.1063/1.1390175

3.5 LDA and GGA
- These methods are fairly affordable for large (100+ atoms) systems
- Local (spin)-Density Approximation (LDA)
- Consider only the local electron density, \(E_{XC} = f(\mathbf{\rho})\)
- Surprisingly good for metals
- Generalised Gradient Approximation (GGA)
- Include local density gradient, \(E_{XC} = f(\rho, \nabla rho)\)
- Better performance for semiconductors and insulators
- Popular GGAs are PW91 and PBE
- We like PBEsol
- Hugely underestimate bandgaps
- DO NOT TRUST BANDGAPS FROM LDA/GGA
3.6 Tight-binding
- Tight-binding models solve a simplified form of \(H\Psi = E\Psi\), where \(H\) contains a minimal set of interactions.
- Calculations are inexpensive and scalable
- The interactions must be parameterised
- "DFTB" refers to automated fitting of a tight-binding model to data from DFT
- Unlike forcefield methods, this is an electronic structure method
3.7 DFT+U
- DFT tends to underestimate on-site Coulomb interactions
- Leads to significant errors for localised d- and f-electrons
- A simple energy correction, \(U\), is included in SCF cycle
- The parameter \(U\) must be sourced responsibly!
- If \(U\) has been fitted to reproduce the experimental bandgap,
then good agreement can be obtained between calculated and measured results.
- This does not mean that good science is being done…
- If a paper uses DFT+U, check where the \(U\) comes from and bear this in mind.
3.8 Hybrid functionals
- GGA functionals tend to under-estimate the "exchange" portion of EXC.
- The Hartree-Fock (HF) method calculates exact exchange, but no correlation.
- Calculated energies can be improved by mixing in some HF exchange
- The main implementations are PBE0 (below), B3LYP (older, very succesful) and HSE06 (PBE0 with range-screening)
- Unfortunately, the scaling of HF is worse than GGA, so calculations become slower
- Generally hybrid functionals give "reasonable" results, approaching "chemical accuracy"
3.9 "Beyond-DFT" methods
- Quasi-particle methods
- \(G_{0}W_{0}\), sc\(GW\)
- Time-dependent DFT (TD-DFT)
- Useful for studying transition states, optical properties
- Post-Hartree Fock methods
- coupled cluster [CCSD, CCSD(T)]
- quantum monte carlo
- configuration interaction (CI)
- Some of these methods are very expensive, poor scaling
- Used for "gold standard" reference calculations
4 Theoretical modeling for kesterites
4.1 Total energy calculations
- Geometry optimisation required
- DFT calcs were key for confirming kesterite ground structure
- Conventional unit cells with LDA, GGA sufficient
- Several papers in 2009
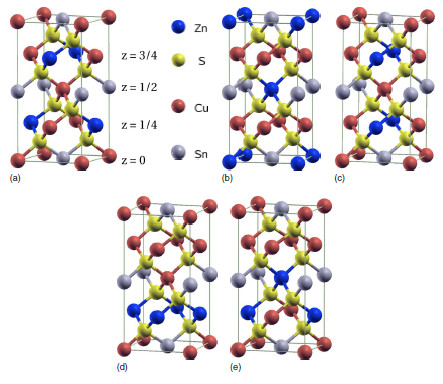 (Paier et al. 2009)
(Paier et al. 2009)

4.2 Defect energies
- By studying larger supercells, simple defects and defect clusters can be studied
- VCu, VCu + CuZn, CuZn + ZnCu clusters shown to have low formation energy

- Defect formation energies depend on energies of other phases; and, ultimately temperature
- Kosyak et al. (2013) combines lattice vibrations with defect formation; finds S vacancies are also likely under annealing conditions

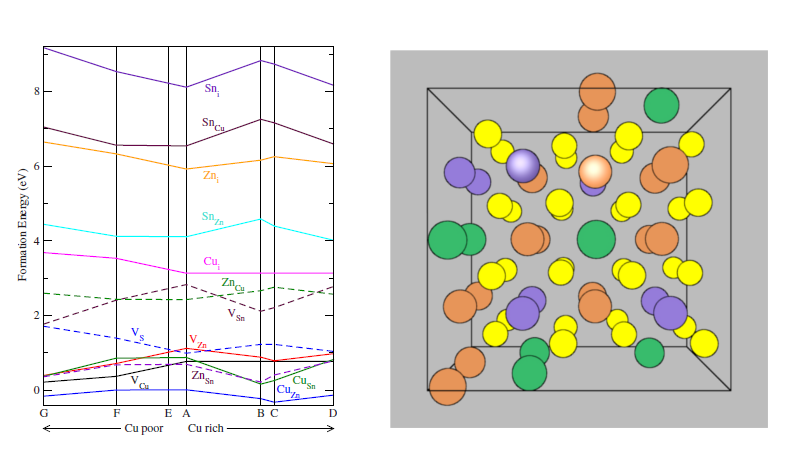
4.3 Bandgaps
- LDA and GGA fail badly
- It is possible to apply an empirical correction or "scissors operator" but
there is no guarantee of accuracy
- This was used by Chen et al. (2009) when looking at CZTS analogues containing Ge
- LDA+U or GGA+U can improve matters, and was used by Persson (2010) for high-quality electronic structure calculations.
- Optimised with LDA for GGA+U calcs
- Est. \(E_g\) 1.5 eV for CZTS, 1.0 eV CZTSe
- From band structure obtain effective masses, dielectric constant, optical absorption coefficient
- Hybrid DFT calculations by Paier et al. (2009) found \(E_g\) 1.49 for kest CZTS, 1.30 for stannite
- Followed up with G0W0 quasiparticle calculation on HSE results, showing little change.
- Expensive!
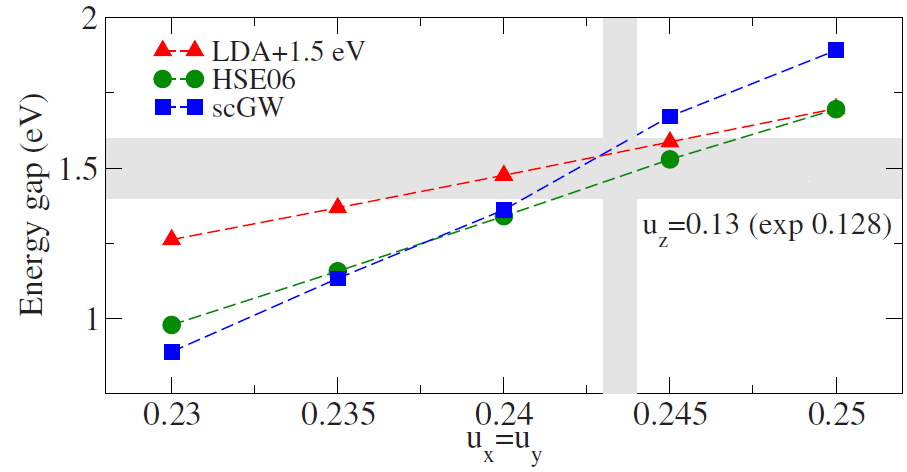
- Botti(2011) compares methods
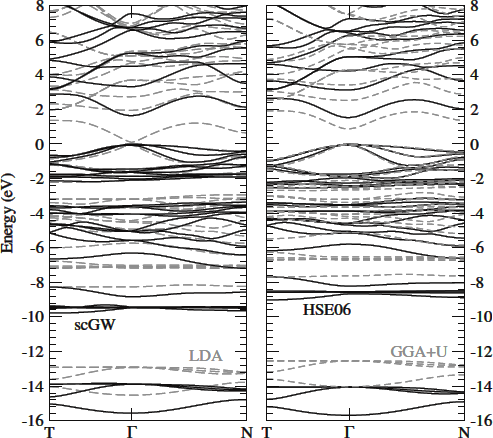
- Same paper shows how sensitive bandgap is to anion displacement
- Shaded regions are experimental values
4.4 Vibrations
- Many theoretical papers say "enthalpy" and mean "ground-state energy"
- Thermodynamic potentials (H, S, \(\mu\) …) are temperature-dependent
- In the solid state this is primarily driven by lattice vibrations
- Some lattice vibrations can be directly observed by IR and/or Raman spectroscopy
4.5 Harmonic approximation
- Assume simple harmonic motion of ground-state lattice
- Two main methods:
- Density functional perturbation theory (DFPT)
- Often quicker, built into many DFT codes. Only gives information at Γ-point.
- frozen phonon method (AKA "direct method" and "supercell method")
- Obtain whole phonon band structure
- Density functional perturbation theory (DFPT)
- Diagonalize matrix of force constants to obtain normal modes and frequencies.
- Results tend to agree qualitatively with experimental frequencies, with errors ~ 10 cm-1
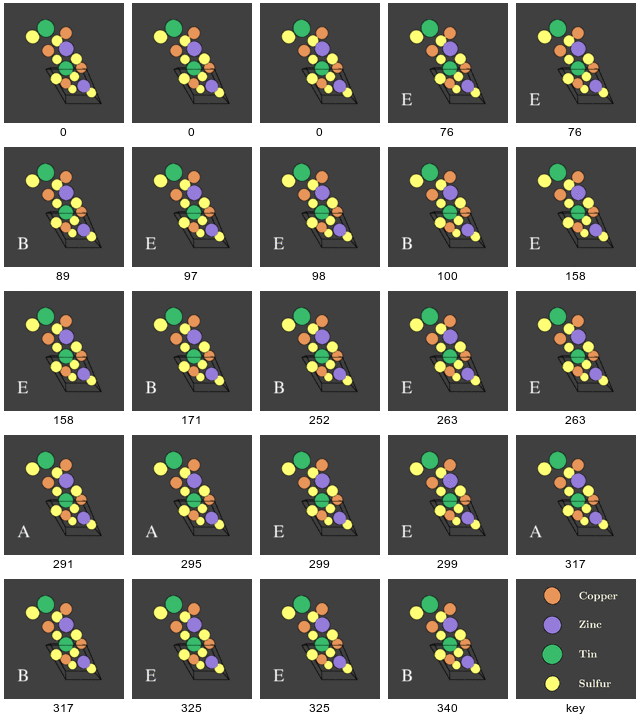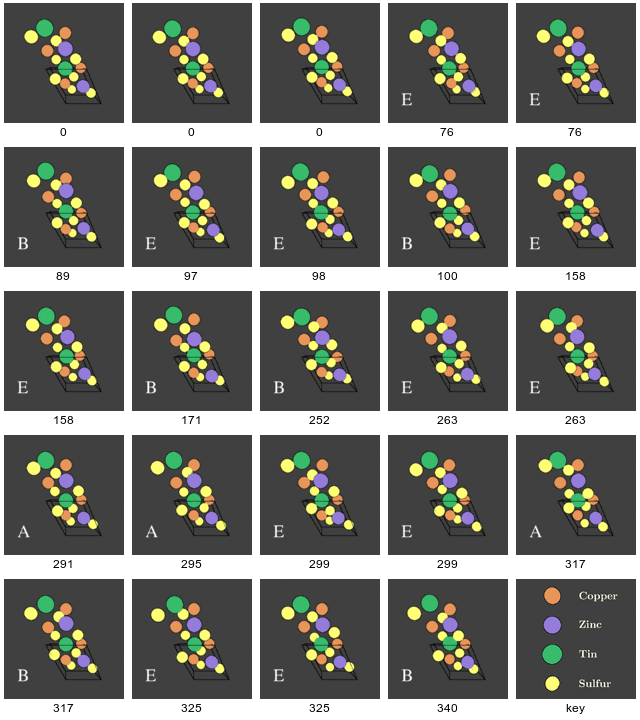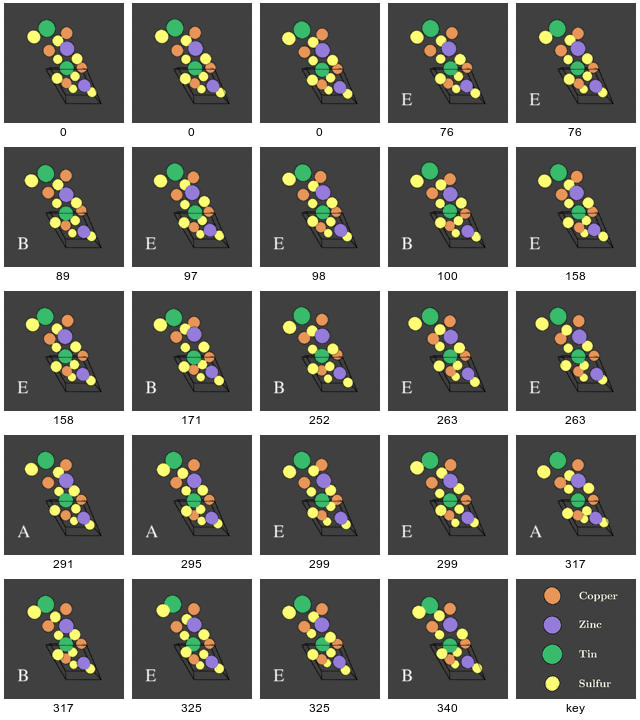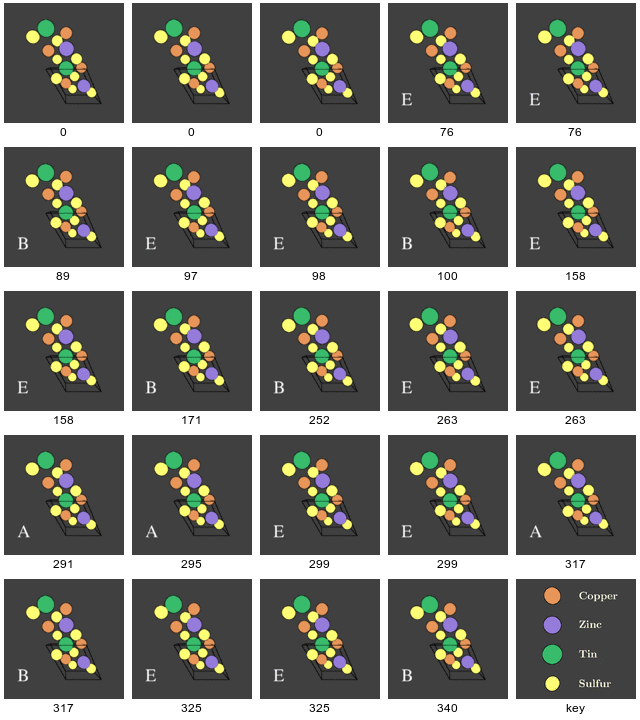
4.6 Beyond the harmonic approximation
- The first step is the quasi-harmonic approximation
- carry out harmonic approximation at several lattice expansions to form Equation of State
- Accounting for thermal expansion tends to "soften" frequencies
- Phonon-phonon interactions
- Very demanding, requires many displacement calculations and slow post-processing
- Allows peaks to be broadened using phonon lifetimes
- For a recent test case we used… CZTS!
- Skelton et al. (2015) improves agreement with IR and Raman data.
- Also shows that CZTS has very low thermal conductivity
5 Some other useful techniques
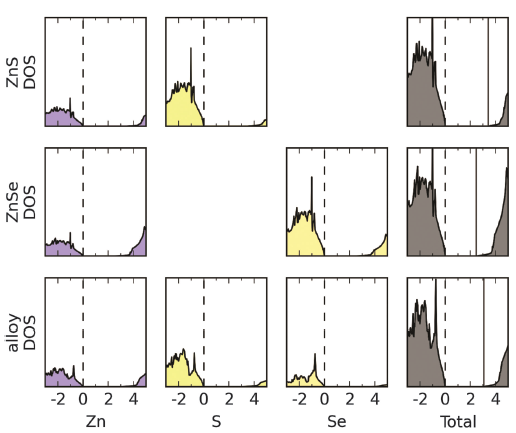
5.1 Projected density of states
- Energy is mapped to atom-centred functions
- Choice of procedures, no "correct" method
- Application: ZnS/Se resonant Raman spectroscopy
- HSE06 hybrid functional used for "good enough" bandgap
- Main challenge was converging k-point mesh

5.2 Surfaces and work functions
- Alignment of valence and conduction bands is important for device design
- Ideal reference point is the vacuum level
- Typical approach is look at electrostatic potential of "slab" models
- Slab cannot be a dipole
- dipole + periodic boundary = infinite energy
- Slab cannot be a dipole
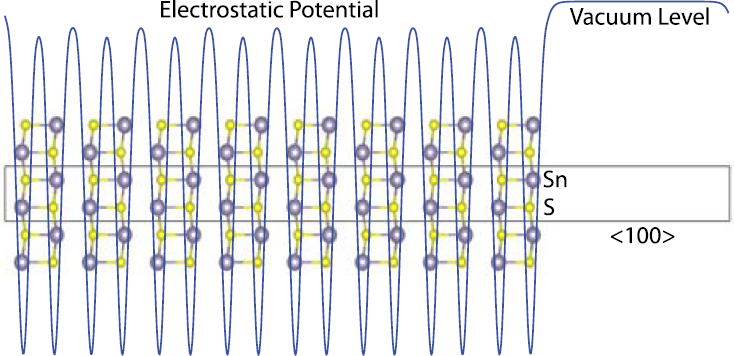
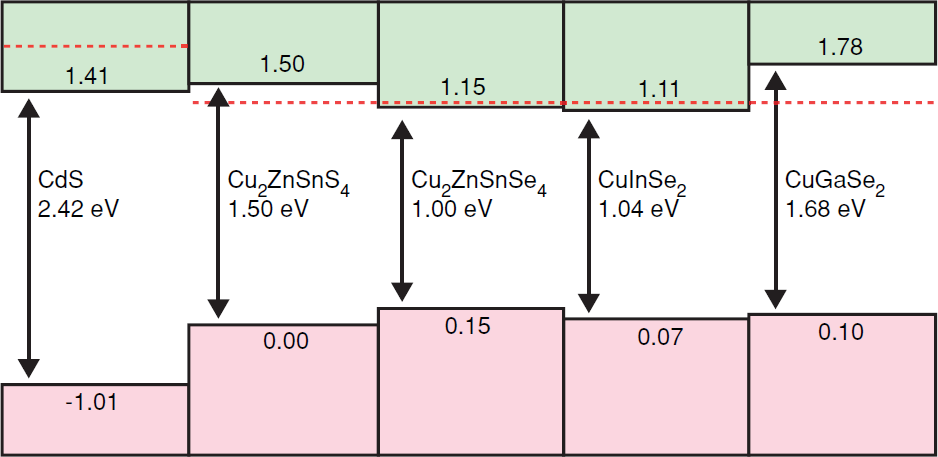
- Band alignment has been done by modelling junctions with CdS and using CdS as the reference. Chen et al. (2011)
5.3 Molecular dynamics
- Calculate forces and follow Newtonian mechanics
- Various methods to introduce temperature
- Many time steps needed for good quality data
- No problem for forcefield models, expensive for ab initio
- We've done some simple tests
- https://www.youtube.com/watch?v=BuvtoyDF4vU
- Activation barrier to disorder is low, but still requires long MD runtimes
6 Wrapping up
6.1 Key work so far
- Ab initio calculations have provided qualitative and quantitative information about the electronic structure of CZT(S,Se)
- Due of scaling challenges we know a lot more about highly-crystalline phases than disordered ones
6.2 Within reason, you can trust
- Lattice parameters (~1%) from LDA or better
- Elastic properties from GGA or better
- Optical properties from GGA+U or better
- Bandgaps from hybrid DFT or better
6.3 Beware
- Optimisation with one method and electronic structure from another
- Conveniently fitted scissors operator or \(U\)
6.4 Some good areas for collaboration
- Γ-point vibrations
- Values for effective mass, absorption
- Properties of well-defined hypothetical materials
6.5 It's hard to help with
- "Fractional" structures
- Bandgaps of disordered, heavily-defective systems
- Surfaces and interfaces - but we must try!
6.6 Acknowledgements
- Centre for Sustainable Chemical Technologies
- PVTEAM
- Computer time from EPSRC, STFC and University of Bath
- Walsh Materials Design group